 |
Древность шахматных игр |
|
|
О появлении шестидесятеричной системы счисления.введение
Счётные африканские доски, видимо, появились, когда система расчётов существовала буквально на земле: создавалась система из лунок в земле в виде двух или трёх рядов. Расчёты велись с использованием подручного материала – семена, орешки, камушки, ракушки. В последующем у тех народов, которые пользовались такими системами расчётов с лунками, появились игры на счётных досках. Количество камней в лунке в начальном положении этих игр связано с определённой системой счисления, практиковавшейся до возникновения этих игр. Наиболее известные игры с лунками на доске – это игры: “манкала” и “вари”. На фото справа игральная деревянная доска из Национального музея Эфиопии в Аддис-Абебе: на доске два ряда противолежащих лунок (по 12 лунок в ряду) с круглыми орешками в лунках.
Реконструкция формирования шестидесятеричной системы счисления в Древнем Междуречье.Современные научные данные говорят, что после великого оледенения на Земле человечество сохранилось как род именно в Африке. При потеплении климата происходило расселение людей из Африки на другие континенты. Такое расселение носило волнообразный характер и происходило двумя путями: по “пешеходным мостикам” между континентами и вдоль побережий с пересечением водных преград морским путём. В районах с благоприятными условиями проживания усиливалась концентрация населения, возникали первые поселения. Наличие пресной воды и возможностей для развития интенсивного земледелия и животноводства, рыбалки, наличие строительного материала (глина и открытая нефть) способствовали появлению оседлого населения в Древнем Междуречье. Первые переселенцы были из Африки и они принесли с собой африканскую культуру. Частью этой древней культуры была двадцатеричная система счисления. Гипотезы о причинах возникновения шестидесятеричной системы счисления.Однако именно в Древнем Междуречье возникла шестидесятеричная система счисления. Загадка её возникновения неоднократно привлекала умы математиков в течение последних двух тысяч лет. Создано несколько гипотез, каждая из которых освещала одну из сторон проблемы. Поэтому каждая из этих гипотез получила свою порцию критики, но это не значит, что они были неверными и не имели жемчужного зерна. Наибольшего внимания, по мнению М.Я. Выгодского, заслуживают гипотезы Тюро-Данжена, Нейгебауера и Веселовского. Они рассмотрены в книге Выготского М.Я “Арифметика и алгебра в древнем мире” (1941, глава 2, параграф 5, стр. 99-104). Кратко об этих гипотезах:
Из гипотез математиков становится ясно, что 60-теричная система возникла на основе ранее существовавшей другой системы счисления. Приведённые выше гипотезы не объясняют, откуда возник позиционный принцип вавилонской нумерации. Реконструкция возникновения новой системы счисления у шумер.Для проведения реконструкции выделим некоторые существенные стороны:
Ключевой вопрос заключается в переходе от одной системы счисления к другой: Как, когда и почему? Изменилась счётная доска или нет? В чём шумеры увидели преимущество 60-теричной системы счисления?Как?! Очень просто. Счётные доски являются универсальными для любой системы. Могут даже одновременно использоваться для самых разных систем счисления! При ознакомлении с главой “Об индийской системе мер” в книге Бируни “Индия” мы сталкиваемся с четверичной системой счисления. Вот цитата из книги Бируни: "Что касается сухих веществ [автор - речь о мерах объема для сыпучих веществ], то для них четыре палы - [одна] кудава, четыре кудавы - [одна] прастха, четыре прастхи - [одна] адхака. Для жидкостей: восемь пал - [одна] кудава, восемь кудав - [одна] прастха, четыре прастхи - [одна] адхака, четыре адхаки - [одна] дрона",- Бируни приводит меры веса, ссылаясь на книгу “Чарака - самхиту”. Я приведу лишь часть названий, исключая ряд промежуточных мер: "Четыре анди - одна маша, четыре маша - одна шана, четыре шана - одна карша (суварна), четыре суварны - одна пала, четыре палы - одна кудава, четыре кудавы - одна прастха, четыре прастхи - одна адхака, четыре адхаки - одна дрона"... Существование в Древней Индии разных систем мер, применение одних и тех же терминов по отношению к различным мерам - это было возможно при использовании счетных досок с лунками, когда каждая лунка имеет определенное название. Тогда попадание камушка (ореха, семечка или раковины каури) в определенную лунку будет названо одним и тем же термином, несмотря на то, что подсчитываться может вес, объем сыпучих веществ, объем жидкости, расстояния, время. Например: термин “пала” в санскрите означает определенную единицу времени, равную приблизительно 24 секундам. Этот же термин “пала” применялся в Древней Индии как мера веса, как мера сыпучих тел, как мера объема жидкостей! В 15 главе книги "Индия" Бируни сделал следующее замечание: "Поскольку единица [меры] в действительности вовсе не является единицей веществ [или предметов], а напротив, она есть количество, которое люди условились называть единицей, // то она допускает практическое и воображаемое деление на части. А эти части различны в различных местах в одно и то же время, и в разное время в одном и том же месте. Их названия [также] меняются в зависимости от времени и места при коренных переломах в языках или при частичных изменениях в них."
Когда? В конце IV тысячелетия до нашей эры в южной части Двуречья начали складываться государственные образования шумеров. Изобретение шумерами письма в виде клинописи, их достижения в области метрологии и математики, литературы и искусства, - всё это определило дальнейшее культурное развитие древней Передней Азии. Но об этом мы узнали только в последние сто лет! В последние 30-40 лет появились новые открытия в археологии Древнего Ближнего Востока, которые изменили взгляд на раннюю историю шумер. Для более детального ознакомления с данным тезисов даю ссылку на статью "Шумер как культурно-историческая система" (автор - Н.В. Козырева) (http://vostokoved.spb.ru/read.php?sname=gudea&articlealias=Sumer_civ) Замечу лишь, что находки датируют от середины 9 тысячелетия до н.э. до 3 тысячелетия до н.э.
О том, что запись чисел осуществлялась в шестидесятеричной система исчисления, исследователи догадались по приводимым в табличках вычислениям. Характерной чертой административных документов были именно вычисления: например, «был 51 теленок, родилось еще 12, итого 63 теленка» Есть ещё одна гипотеза для обоснования выбора числа 60 в качестве основания новой системы счисления. Это гипотеза Кантора о его "астрономическом" происхождении. "Происхождение числа 60 в качестве основания вавилонской системы счисления, а также чисел 12, 30 и 360 как узловых чисел всех календарных систем, систем измерения времени и угловых величин можно объяснить с позиций астрологических и астрономических знаний и основанных на них представлений о гармонии Вселенной. В Вавилоне и Египте с давних времен при составлении календарей большое значение придавали самой крупной из планет-гигантов - Юпитеру, который примерно за 12 лет делает полный оборот вокруг Солнца. Не меньшую роль играл также Сатурн, который совершает полный оборот вокруг Солнца примерно за 30 лет. Приняв 60 лет в качестве главного цикла Солнечной системы, составителям древних календарей удалось идеально согласовать циклы Юпитера (5x12=60) и Сатурна (2x30=60)". Учитывая время появления шестидесятеричной системы счисления- 32 век до н.э., данная гипотеза должна предполагать наличие у шумер выдающихся знаний астрономии, совершенной календарной системы, письменной передачи знаний, так как наблюдение 60-летних циклов выходило за пределы одной человеческой жизни. Кантор впоследствии отказался от своей гипотезы и принял гипотезу Г.Кевича.
Почему? На этом вопрос нужно отвечать сразу с двух позиций (и математики и истории). С позиций истории. Снова обратимся к статье Н.В. Козыревой. Шумер впервые предстает перед нами во второй половине 4-го тысячелетия как союз городов-государств, объединенных единой идеологией и определенной хозяйственной общностью. Эта хорошо сбалансированная и внутренне устойчивая система для внешнего наблюдателя представляется невероятно сложной сетью соединенных между собой функций, прав и обязанностей. Каждый отдельный город-государство представлял собой в свою очередь достаточно сложную структуру, состоявшую из больших и малых самоснабжающихся хозяйств, в центре каждого из которых находился храм. В рамках этих храмовых хозяйств были заключены все территориальные, материальные и людские ресурсы данного города. Такая хозяйственная система была неразрывно связана с религиозными представлениями шумеров. Можно предположить, что представления о божестве в Шумере были изначально неотделимы от представления о контроле над определенным участком земной поверхности, подразумевалась тесная связь божества с определенной территорией, и наоборот, территория каждого города и все, находившееся на данной территории, принадлежало богу данного города, составляя его хозяйство, или Дом. Границы каждого города-государства считались установленными и санкционированными богами, и поэтому любая попытка территориальной экспансии была, по существу, нарушением божественной воли и вследствие этого была достаточно затруднительна. В рамках такой идеологии теоретически немыслимой была бы идея унификации, создания единого территориального государства с централизованным управлением. Земледелие, скотоводство, а так же ремесленное производство велись в рамках храмовых общин коллективно. Производимые продукты централизованно собирались, хранились и затем различными способами распределялись между членами этих хозяйств. Экономику такого типа, следуя теории Карла Поляни, можно назвать преимущественно распределительной. То есть, нам надо отказаться от гипотез, связанных с изменениями системы счисления в угоду торговли или же в связи с введением налогов в рамках централизованного государства. Как всегда, когда мы распределяем, то надо делить произведённую продукцию на всех членов общества. Общество носило отчетливо эгалитарный характер (лат.egalis - равный). Все жители, обитавшие на территории храмовой общины, составляли персонал храмового хозяйства, и все они, независимо от пола, возраста и количества выполняемого труда, могли рассчитывать на материальное содержание от храма. Характер этого содержания по количеству и качеству безусловно зависел от положения того или иного лица в должностной иерархии, но не мог быть ниже необходимого прожиточного минимума. С позиций математики древнего мира: Деление - более сложная задача, чем сложение и вычитание или умножение. При существовании двадцатеричной системы натуральные делители: 1, 2, 4, 5, 10 делят число 20 без остатка. Основание двадцатеричной системы - число 20 совершенно не подходит для деления на 3 (простое число!) - появляются "ломанные числа", то есть дроби. Если деление необходимо каждодневно (в связи с распределительной системой экономики), то избежать этих "ломанных чисел" можно лишь увеличив основание системы - на множитель 3. При этом увеличении система счисления получает новое основание - 60. И это основание на практике доказывает свою полезность, так как оно имеет максимальное количество делителей из натуральных чисел: 1,2,3,4,5,6,10,12,15,20,30,60. Кроме этой причины (с позиций математики) для смены системы счисления, возможно, была и сопутствующая причина - связанная с "упрощением" или укорочением записи чисел. У шумер возникла необходимость записи всё больших чисел, которые в двадцатеричной системе потребовали бы громоздких записей. На этот момент до сих пор никто не обращает внимание. Сложение или вычитание не требуют изменять основание системы счисления. Умножение? - есть даже определённые неудобства при увеличении основания системы до 60. На это указал Марк Яковлевич Выгодский в книге "Арифметика и алгебра в древнем мире" (стр.106): "Вавилонский приём умножения по существу совпадал с современным. Но в то время как нам приходится запоминать таблицу умножения, содержащую 36 небольших по величине (2x2,2x3,2x4 ... 3x4,3x5... 9x9) результатов, вавилонскому вычислителю, если он хотел бы сразу написать частичное произведение разряда на разряд (до 59x59), требовалось бы помнить 1711 результатов, выражающихся громоздкими числовыми образованиями. Естественно, что ему пришлось прибегать таблице умножения." Вавилонская математика пользовалась теми же приёмами при делении, которые изобрели шумеры. Деление m/n они заменяли умножением m ×(1/n), а для нахождения 1/n у них были специальные таблицы (таблицы обратных величин). О том как решалась проблема №1 (!), то есть деление, подробно написано в 1томе "Истории математики с древнейших времён до начала XIX столетия" (в трёх томах) под редакцией А.П. Юшкевича [Изд. "Наука", 1970 год, 37-39 страницы] Изменения счётной доски при переходе от 20-теричной к 60-теричной системе счисления: Сама счётная доска не изменилась совсем. Произошло перераспределение счётного материала для разрядных лунок. В двадцатеричной системе в первой лунке (крайняя справа) считали до 5 ("пятирили") пальцев, а во второй (считая слева направо) считали до четырёх ("четверили" по числу конечностей одного человека), то есть счёт в двух лунках первого разряда вёлся до 20. В следующем разряде считали аналогично в двух лунках, но "пятирили" уже "двадцатки". О том, что шумеры "пятирили", говорят названия цифр: при дешифровке шумерского языка оказалось, что “семь” (имин) звучит как 5 + 2 (5 = иа + 2 = мин ), а девять ( иллиму ) - как 5 + 4 (5 = иа + 4 = лимму ) (“История математики”, т.1-й, изд. ”Наука” М.1970 стр.11). "Пятирили" шумеры при двадцатеричной системе счисления! Ниже приведены количественные числительные по статье Шумерский язык на сайте Википедия. Видно, что числительные 30, 40, 50 образованы тоже под влиянием использовавшейся ранее двадцатеричной системы! Количественные числительные.
При увеличении основания до 60 пятирить уже нет смысла, так как во второй лунке будут дюжины! Но при использовании счётной доски отход от пальцевого счёта закономерен. У шумер же перестали "пятирить", а взамен этого стали "десятирить" в первой лунке. Вторая лунка вовсе потеряла связь с пальцевым счётом! - в ней стали считать до 6 (десятков). Счёт десятками не был раньше появления шестидесятеричной системы! Имено поэтому у шумер отсутствуют названия некоторых чисел, характерных для десятеричной системы. К данной гипотезе меня привело предположение, что "счётные игры" Африки древнее 3-го тысячелетия до н.э., что они появились из практической деятельности и первоначальное их предназначение - счётные доски для двадцатеричной системы счисления. При раскопках древнейших городов долины Инда была найдена доска с возрастом более 4500 лет, в которой применялись круглые камешки и бобы. Об этой находке английский археолог Э. Маккей пишет, что “все устройство в высшей степени напоминает игральную доску, распространенную в различных африканских племенах”.(Э. Маккей “Древнейшая культура долин Инда”, М., изд.Иностр. лит.,1951,с.123) По поводу влияния математики Шумер на сохранение позиционного принципа в разных системах счисления.Китайский математик третьего века Сунь-цзы: ”В методах, которые употребляются при обычном счете, прежде всего [следует] познакомиться с разрядами: единицы вертикальны, десятки горизонтальны, сотни стоят, тысячи лежат, тысячи и десятки выглядят одинаково, десятки тысяч и сотни - тоже”. Сунь-цзы “Математический трактат”. Перевод Э.И.Березкиной. “Из истории физико-математических наук в станах Востока”, 1963, вып. 3, 23 . Слова Сунь-цзы о применении позиционного принципа к десятичной системе счисления в Китае напоминают мне один к одному о шумерской клинописи только для шестидесятеричной системы. Последовательная запись чисел по возрастанию в десятичной системе мы ведём справа налево в порядке: единицы - десятки - сотни - тысячи. При чтении числа мы читаем его слева направо - в порядке убывания разрядов. Например, 1984 г. - тысяча девятьсот восемьдесят четвёртый год. Так вот, это возрастание разрядов справа налево мы тоже наследовали из математики Шумер. Конечно, запись числа шумеры вели, привязывая разряды к лункам доски, но ведь и возрастание разрядов на их счётной доске шло справа налево.. Видимо, это шло от пальцевого счёта: "пятирили" правой рукой, "четверили" - левой. Следующий человек, считающий двадцатки, должен был стоять левее первого и смотреть на его левую руку. Использованы материалы: 5.02.2013 Шиляев А. |
Устный счёт появился раньше письменности. Известно, что у многих народов ещё до появления письменности были математические знания, которые передавались изустно. В Африке у многих народов для производства расчётов использовались специальные доски. Суть этих досок аналогична более известному абаку.
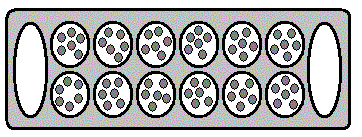
Cчётные маркеры из глины, Сирия / Шумер / Хайленд Иран, ок. 8000-3500 до н.э., 3 сферы: диам. 1,6, 1,7 и 1,9 см, (DS-B 2:1); 3 диски: диам. 1,0х0,4 см, 1,1x0,4 см и 1,0х0, 5 см (DS-B 3:1); 2 тетраэдры: бока 1,4 см и 1,7 см (DS-B 5:1).
на фото справа: MS 4647, Сирия / Шумер / Хайленд Иран, ок. 3500-3200 до н.э., 4,4x5, 3 см. Появляются счётные таблетки с числами, обозначенными более сложной комбинациией разрядов, что являются ещё одним шагом перехода от бирки к простейшей форме счета в корреспонденции. Такие глиняные таблетки использовались параллельно с Булла-конвертами (с жетонами внутри). Известно приблизительно 260 числовых таблетки. Большинство из них находятся в Иране.
Старо-шумерская клинопись на глиняной "таблетке", Шуруппак, Шумер, 27 столетие до н.э., по 1 таблетке, 7,2 х7, 1х2, 0 см, 28 карманов в клинописи. Данная археологическая находка расценивается как пример геометрической прогрессии.
Вавилония, ок. 19 в. до н.э. MS 2221 (4,5x11, 7x2, 8 см, один столбец, 2 строки в клинописи). Очень большое 15-разрядное шестидесятеричное число [13 22 50 54 59 09 29 58 26 43 17 31 51 06 40], эквивалентное 20-й степени числа 20, что = 104.857.600.000.000.000.000.000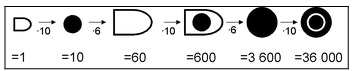
Очевидно, что переход от двадцатеричной системы счисления к 60-теричной произошёл в период роста и расширения границ шумерской цивилизации - точнее с 35 по 32 век до н.э. Именно в этот период возникла потребность в удобной компактной записи больших чисел и проведении с ними арифметических действий. Первые же документы, написанные несомненно на шумерском языке, происходят из Джемдет-Насра (культура раннего бронзового века) и датируются 3200–3100 гг. до н. э. В Уруке обнаружены несколько сот глиняных табличек, большая часть которых датируется 3200–3100 гг. до н. э. Начиная с архаического периода и до конца существования месопотамской цивилизации, в текстах засвидетельствована шестидесятиричная система исчисления, представленная на рисунке. При обозначении любого числа знаки писались по убывающей.("Языки мира: Древние реликтовые языки Передней Азии" М.: Academia, 2010) В этот период также происходит урбанистическая революция: многочисленные мелкие поселения Месопотамии превращаются в крупные города.