Математика древнейших цивилизаций Африки, Др. Междуречья, Др. Индии и её связь с настольными играми.
(Легенда о награде изобретателю шахматной игры, проверка её методами древней математики)
Часть 1.
- A. Обучение счету на досках в древности.
- B. Двадцатериричная система счисления и игры семейства вари.
- C. Шестидесятиричная система в Ассирии и игры семейства манкала-калах.
- D. Рождение десятеричной системы в Индии.
- Африка - родина древних игр переноса (вари, манкала, паллангули, тогыз-кумалак и другие).
- Игровые доски и их связь с разными системами счисления.
Часть 2.
- Легенда о награде изобретателю шахматной игры, проверка её методами древней математики.
- Тогыз-кумалак. Казахская игра - свидетельство зарождения десятиричной системы счисления.
- Буддийская "колесница" в индийских играх (Чатуранга, Рума).
- Компьютер и игры переноса.
Африка - родина древних игр переноса.
 В Лондоне, в Британском музее, хранится загадочная бронзовая статуэтка африканского короля Шамба Болонгонго (Shamba Bolongongo), найденная в Бакума (Bakuma) и датируемая началом семнадцатого века. Статуэтка выполнена в натуралистическом стиле высотой 54 см. Король сидит, скрестив ноги, на небольшом возвышении. Руки опущены на колени, в левой руке свиток, спина выпрямлена, лицо спокойно и не выражает эмоций. Лицо типичное для жителя Нигерии. Поза... Если бы это был индийский йог, то эту позу можно было бы назвать одним санскритским словом surhasana (сурхасана) или поза удовольствия. Перед королем у его ног находится необычный предмет овальной формы с девятью круглыми углублениями в центре и двумя полукруглыми углублениями по сторонам.
В Лондоне, в Британском музее, хранится загадочная бронзовая статуэтка африканского короля Шамба Болонгонго (Shamba Bolongongo), найденная в Бакума (Bakuma) и датируемая началом семнадцатого века. Статуэтка выполнена в натуралистическом стиле высотой 54 см. Король сидит, скрестив ноги, на небольшом возвышении. Руки опущены на колени, в левой руке свиток, спина выпрямлена, лицо спокойно и не выражает эмоций. Лицо типичное для жителя Нигерии. Поза... Если бы это был индийский йог, то эту позу можно было бы назвать одним санскритским словом surhasana (сурхасана) или поза удовольствия. Перед королем у его ног находится необычный предмет овальной формы с девятью круглыми углублениями в центре и двумя полукруглыми углублениями по сторонам.
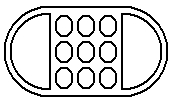 Что же это за предмет!? Символ государственной власти или магических знаний? Прибор для письма, для смешивания красок? Ни то, ни другое. Это счетная доска, древнейший калькулятор времен неолита, отлитый в бронзу. Счет на такой доске аналогичен счету на древнеримском абаке или древнеиндийской вычислительной доске патигоните. Необычный предмет у ног короля - это символ математических знаний, которыми он гордился.
Что же это за предмет!? Символ государственной власти или магических знаний? Прибор для письма, для смешивания красок? Ни то, ни другое. Это счетная доска, древнейший калькулятор времен неолита, отлитый в бронзу. Счет на такой доске аналогичен счету на древнеримском абаке или древнеиндийской вычислительной доске патигоните. Необычный предмет у ног короля - это символ математических знаний, которыми он гордился.
Доски с лунками известны и в современной Африке, только используются они для игр. Это игры переноса или манкальские игры. Очевидно, что специальные игровые доски появились позднее, чем сами эти игры. Для игры достаточно сделать в определенном порядке несколько углублений на земле и собрать необходимое количество камушков (или ракушек, или горошин, или орехов...) Ход заключается в том, игрок вынимает все камни из одной лунки и по одному раскладывает их в другие лунки - последовательно, начиная с соседней, не пропуская ни одной.
Древность этого типа интеллектуальных игр на досках не вызывает сомнений. Родословная игр переноса на несколько тысячелетий древнее шахмат и древнее китайской игры вейци (го- японское название). Распространенность игр переноса первым отметил американский ученый и исследователь игр Стюарт Кулин (Culin S , 1858-1929) Он в 1896 году написал работу под названием "Манкала, национальная игра Африки". Под разными названиями манкальские игры имеют хождение во многих странах Азии. Например, халуза (в Месопотамии), паллангули (в южной части Индии и Шри-Ланка), джонгкак (в Малайзии), тогыз-кумалак (в Казахстане). Игры переноса попали в Америку в колониальный период из Западной Африки. Соплеменники Шанго Болонгонго сохранили на новой родине национальные игры. Роберт Белл предположил, что можно "проследить корни некоторых вест-индских негров по тому, какую форму манкалы они предпочитают”. Европейцы впервые познакомились с манкалой после издания в 1694 году книги Томаса Хайда, в которой впервые приведено описание двух форм этой игры. Считается, что "манкала” получила свое название от арабского слова "накала”, что в переводе означает "переносить из одного места в другое”. Возможно, что слово "манкала” надо переводить с санскрита (ман - размышлять, кала - счет, время). При таком переводе выявляется другое значение: вычислять, измерять, следить за временем. В англоязычной литературе слово "манкала” принято в качестве родового понятия всех игр переноса.
Трудно даже предположить, как давно произошло замена пальцевого счета на счет камушками. Однако это сразу раздвинуло возможности для арифметических действий. Не случайно в комедии Аристофана (ок.445-ок.385 гг. до н. э.) "Осы” говорится: "Подсчитаем попросту, не на камушках, а на руках, все подати... ” По-видимому, пальцевым счетом владели тогда многие, но не все могли произвести расчеты с помощью более прогрессивного способа. Обучение афинского мальчика описано в книге К. М. Колобова и Е. Л. Озерецкой "Как жили древние греки” (М., 1959 г., стр.201): "Проходили долгие месяцы, прежде чем мальчик выучивался прилично считать и писать. Платон отводил на это школьнику три года. Быстрее шло дело с арифметикой. Она преподавалась наглядно и не утомительно, с помощью яблок, пальцев и др. пособий. Больше всего помогала абака - род счетной доски с углублениями, разграничивавшими единицы, десятки и сотни. В углублениях располагали камешки, имеющие то или иное номинальное значение, и с ними наглядно производились арифметические действия не только с целыми числами, но и с дробями”. Один и тот же камешек на абаке мог означать и единицы, и десятки, и сотни, и тысячи – в зависимости от его положения на счётной доске. Чаще всего абаком пользовались для денежных расчетов. В Древней Греции бытовала шутка: "Придворный похож на камешек для абака: захочет счетчик, цена ему будет целый талант, а захочет – только хальк".
Пальцевой счет положил начало четверичной системе исчисления (4 пальца = захват лука), пятеричной (одна рука), двадцатеричной (по пальцам рук и ног или по разному положению пальцев кистей), десятичной (по пальцам обоих рук).Счет предметов производили чаще всего с помощью пальцев. Поэтому самыми распространенными являются десятеричная или двадцатеричная системы счисления. Появление шестидесятеричной системы счисления в древнем Вавилоне можно объяснить только появлением счетных досок с камушками в лунках.
Можно предположить, что в становлении и десятичной, и шестидесятеричной систем счисления доски с камушками сыграли главную роль. Необходимость зафиксировать полученный результат вычислений на доске привела к появлению цифр и числовой записи. Например, запись числа 2727 римскими цифрами будет выглядеть так: ММДССХХVII (1000 + 1000 + 500 + 100 + 100 + 10 + 10 + 5 + 1 + 1). Числа, записанные римскими цифрами, не удобны для вычислений. Попробуйте, например, умножить вышеназванное число на LXXXIV , пользуясь римской системой. Чтобы узнать, как производили вычисления в Др. Риме и происхождение римских цифр, пройдите по ссылке http://igor-grek.ucoz.ru/publ/lux/schet_2/15-1-0-450
Арабские цифры пришли к нам из Индии. Это были первые буквы названий от 1 до 9 (на санскрите). Первоначально этими буквами также записывали только промежуточные и конечные результаты расчетов. Но благодаря использованию позиционной системы записи и изобретению нуля (индийские названия нуля - шунья и кха) числа стали использоваться и в процессе арифметических действий. В последствии счетные доски с камушками перестали использоваться. Правда, счёт на досках в XIX и XX веках продолжал использоваться в виде приборов: русские счеты, китайский суаньпань, японский соробан.
Вычисления на досках с камушками проводились по позиционному принципу, который использовался и в древнеримском абаке. На следующем примере показана последовательность выполнения сложения на абаке: 348 + 164 = 512
Вычисление суммы .
1-й шаг. ( 3 )( 4 )( 8 ) +
( 1 )( 6 )( 4 )
2-й шаг. ( 4 )( 10 )(12)
3-й шаг. ( 4 )(10+1)( 2)
4-й шаг. (4+1)( 1 )( 2 ) Результат: 512
Вычитание осуществляется изъятием камешков, умножение - как повторные сложения, деление - соответственно повторными вычитаниями. Все, что касается десятичной системы и вычислений в ней, не требует комментариев даже при использовании абака, т.е. доски, разделенной вертикальными линиями для разрядов. Переход на один шаг влево увеличивает значение в десять раз.
Позиционная система записи чисел до утверждения ее в Индии уже существовала у древних шумер. Это подтверждено дешифровкой книг по математике из библиотеки Ашшурбанипала, царя Ассирии в 669 - ок.633 до н.э. Выяснилось, что почти за 2000 лет до н.э. были составлены таблицы умножения, квадратов последовательных целых чисел. Для решения квадратных уравнений народы Месопатамии разработали систему действий, эквивалентную современной формуле. Но не были найдены рассуждения, приведшие к используемому алгоритму, т. е. математику Древнего Вавилона можно было назвать рецептурной, хотя неизвестно, каким образом были получены эти рецепты. В одной из своих надписей Ашшурбанипал хвастает, что он "умеет решать сложнейшие задачи на умножение и деление”. Наших знаний о позиционной системе достаточно, чтобы решить любые примеры на сложение, вычитание и действия с дробями. Однако, при обращении к клинописным таблицам современный человек сталкивается с непониманием нескольких несложных проблем
Следы вавилонской нумерации сохранились до сих пор: 1 час = 60 минут, 1 минута = 60 секунд; аналогично при делении окружности на градусы, минуты, секунды. Такая традиция пришла из астрономии. Вавилоняне проводили систематические наблюдения за звездным небом, составляли календарь, вычисляли периоды обращения Луны и всех планет, могли предсказывать солнечные и лунные затмения. Эти знания астрономии впоследствии перешли к грекам, которые вместе с астрономическими таблицами заимствовали и шестидесятеричную нумерацию.
Давайте вместе рассмотрим особенности ассиро-вавилонской математики.
Ассиро-вавилонская математика пользовалась (помимо десятичной) шестидесятеричной системой счисления, в основу которой положено число 60 (или 6×10). Это число играет такую же роль при переходе к следующему разряду, как и число 10 в десятичной системе.
Для записи чисел вавилоняне использовали всего два клинописных символа:
- 1.
 вертикальный или прямой клин обозначал единицу(60°), но он же мог обозначать 60 в первой степени, если за ним находился лежачий клин , или число 3600 (60²), или даже 216000 (60³).
вертикальный или прямой клин обозначал единицу(60°), но он же мог обозначать 60 в первой степени, если за ним находился лежачий клин , или число 3600 (60²), или даже 216000 (60³). - 2.
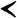 горизонтальный или лежачий клин обозначал десяток, но мог в разных положениях при записи чисел обозначать также 600 и 36000.
горизонтальный или лежачий клин обозначал десяток, но мог в разных положениях при записи чисел обозначать также 600 и 36000. -
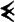 этот символ для обозначения нуля появился позднее.
этот символ для обозначения нуля появился позднее.
Шумеры, создавшие шестидесятеричную систему, знали устройство африканских счетных досок с лунками. Они заменили двадцатеричную систему счисления шестидесятеричной, не изменив при этом строение счетной доски. Выбор числа 60 в качестве основания для новой системы счисления объясняется просто. Число 60 имеет максимальное количество делителей (из чисел от единицы до 100) для деления без остатка: 1,2,3,4,5.6,10,12,15,20,30. Благодаря этому упростились действия с дробями, а математики древнего Вавилона вошли в историю как первые, кто стал использовать систематические шестидесятеричные дроби, и как первые, кто ввел знак для обозначения пропущенного разряда (удвоенный по вертикали лежачий клин).
Чтобы дешифровать число 

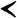
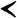

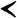


 [ 2;21;13] в десятичную систему, необходимо сложить значения всех знаков. 3600 + 3600 + 600 + 600 + 60 + 10 + 1 + 1 + 1= 8473. Как же должна была выглядеть доска для вычислений в Ассирии?
[ 2;21;13] в десятичную систему, необходимо сложить значения всех знаков. 3600 + 3600 + 600 + 600 + 60 + 10 + 1 + 1 + 1= 8473. Как же должна была выглядеть доска для вычислений в Ассирии?
Во-первых, должно быть деление на разряды. Каждый последующий разряд был в 60 раз больше предыдущего.Точно так же, как и в десятичной системе, в шестидесятеричной для каждого разряда существовали свои названия. Их можно восстановить по названиям весовых мер: 60 шекелей = 1 мина; 60мин = 1 талант или временных мер: 60 минут (2 вавилонских двойных часа) = 1 мина (или одна стража); 6 мин = 1 сутки Таким образом, первые 3 разряда последовательно назывались: шекель - мина - талант. Самым крупным разрядом был талант. Именно это название использовалось в Вавилоне, Персии, Древней Греции, Египте для обозначения самой большой весовой и денежной меры. Вторым по значимости был разряд мина. Еще меньше - шекель. Всего было три разряда, которые соотносились друг к другу следующим образом:
1 талант = 60 мин = 3600 шекелей; 1 мина = 60 шекелей.
Во-вторых, в каждом разряде должно быть два отделения, для разделения "единиц” и "десятков” соответственно клинописным символам  и
и 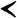 Если для каждого клинописного знака открыть на счетной доске соответствующую счетную лунку, то мы получим ряд из шести лунок (для трех разрядов по два отделения).Оправдывается предположение, что в вавилонской математике все должно быть кратно шести, и отделений тоже было шесть.
Если для каждого клинописного знака открыть на счетной доске соответствующую счетную лунку, то мы получим ряд из шести лунок (для трех разрядов по два отделения).Оправдывается предположение, что в вавилонской математике все должно быть кратно шести, и отделений тоже было шесть.
Однако, один ряд счётных лунок может использоваться только для последовательного счёта или простых арифметических подсчётов. Для сложных действий на доске необходимо открыть параллельный ряд лунок для контроля за количеством счетного материала.Из чисто практических соображений необходимо дополнительно открыть одну или две лунки для складирования камушков, которые то выбывают из подсчётов, то возвращаются в них.
Таким образом, ассирийский абак должен был состоять из счётных лунок, расположенных в два параллельных ряда с шестью лунками в каждом, с добавлением одной - двух лунок для складирования счётного материала, расположенных отдельно:
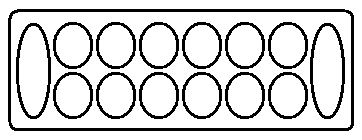 В двух крайних лунках справа происходит накапливание камушков до 60. Сначала в крайней правой лунке накапливается до 9 камушков, при попадании в эту лунку ещё одного или нескольких камушков, десяток их вынимается и один камушек (при сложении) опускается в соседнюю лунку слева, где счет идет до 6 десятков. При попадании шестого все камушки из этой лунки вынимаются, и один из них опускается в лунку следующего разряда. Фактически на счётной доске для счёта в каждом разряде использовались две лунки: "правая" для счёта "единиц", а "левая" - для счёта десятков.
В двух крайних лунках справа происходит накапливание камушков до 60. Сначала в крайней правой лунке накапливается до 9 камушков, при попадании в эту лунку ещё одного или нескольких камушков, десяток их вынимается и один камушек (при сложении) опускается в соседнюю лунку слева, где счет идет до 6 десятков. При попадании шестого все камушки из этой лунки вынимаются, и один из них опускается в лунку следующего разряда. Фактически на счётной доске для счёта в каждом разряде использовались две лунки: "правая" для счёта "единиц", а "левая" - для счёта десятков.
При записи числа для каждой лунки при записи использовалось своё обозначение. Однако, позднее для ускорения и упрощения записи поняли, что достаточно только двух знаков (для левой и правой лунки), так как запись числа производилась последовательно и повторение знака в другом разряде не вносит путаницы.
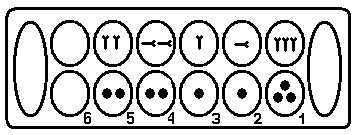 Воспроизведение клинописного числа
Воспроизведение клинописного числа 

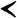
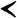

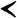


 [ 2;21;13] (в десятичной системе число 8473) на счётной доске - это несложная задача. В крайнюю правую лунку, соответствующую вертикальному клину, укладываются 3 камня (III).
[ 2;21;13] (в десятичной системе число 8473) на счётной доске - это несложная задача. В крайнюю правую лунку, соответствующую вертикальному клину, укладываются 3 камня (III).
Затем идёт раскладка камней в лунки слева направо с чередованием их соответствия вертикальному или горизонтальному клину.
В следующей таблице дано обозначение одного камня и его "вес” в десятичном счислении.
| Номер лунки (слева направо) | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|
| Клинописный знак | 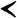 |
 |
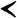 |
 |
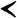 |
 |
| Значение в десятичной системе | 36000 | 3600 | 600 | 60 | 10 | 1 |
| Название разряда в шестидесятиричной системе | Талант | Мина | Шекель | |||
При заполнении лунки счётной доски, соответствующей вертикальному клину,- до 10 - необходимо все камни из неё вынуть и один положить в следующую разрядную лунку слева, а остальные перенести в резервную или накопительную лунку.
При заполнении лунки счётной доски, соответствующей лежачему клину, - до 6 - необходимо все камни из неё вынуть и один положить в следующую разрядную лунку, а остальные перенести в резервную или накопительную лунку.
Древние греки заимствовали систему весовых мер с Востока:
- 1 талант = 60 мин = 6000 драхм;
- 1 мина = 100 драхм = 600 оболов;
- 1 драхма (горсть)= 6 оболов; 1обол (прут)=12 ячменных зёрен.
"Первым из греков завел точные меры, вес и монету аргосский царь Фиждон. Это была первая система мер в Европе.
- стадий = 100 охватов ок. 180 м
- охват = 4 локтя - 6 ступней ок. 1 м 85 см.
- локоть = 2 пяди - ок. 46 см 2 мм
- ступня = 4 ладони - ок. 30 см 8 мм
- пядь = 12 пальцев ок. 23 см 1 мм
- ладонь = 4 пальца - ок. 7 см 7 мм
- палец = ок. 1 см 9 мм
И удобство, и неудобство этой системы сразу бросается в глаза. Удобство - в том, что все единицы почти точно соответствуют размерам человеческого тела. Неудобство - в том, что пересчет из одних единиц в другие очень громоздок”...
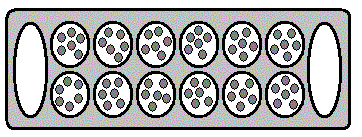 Одна из игр переноса - калах - имеет устройство доски, совпадающее с устройством ассиро-вавилонского абака. Не надо искать объяснение данного названия за пределами Месопатамии. Известно, что Калах - Кальху- крупнейший город Ассирии, основанный царём Салманасаром I в XIII в.до н э. на левом берегу Тигра, совр. городище Нимруд в Ираке. В XIII-XI и в IX-VIII в.до н.э. был столицей Ассирии. В конце VII в.до н.э. разрушен мидянами и вавилонянами.
Одна из игр переноса - калах - имеет устройство доски, совпадающее с устройством ассиро-вавилонского абака. Не надо искать объяснение данного названия за пределами Месопатамии. Известно, что Калах - Кальху- крупнейший город Ассирии, основанный царём Салманасаром I в XIII в.до н э. на левом берегу Тигра, совр. городище Нимруд в Ираке. В XIII-XI и в IX-VIII в.до н.э. был столицей Ассирии. В конце VII в.до н.э. разрушен мидянами и вавилонянами.
Начальная расстановка камней в игре калах: на доске 6 пар противолежащих лунок, в каждой лунке по 6 камней. Правила игры в калах просты настолько, что их осваивает ребенок 5-8 лет . Вместо специальной доски с лунками можно использовать пластмассовые коробочки, вместо камней - горошины или бобы. Главное, чтобы их было 72 (6 х 12). Игра для двух человек. Ход заключается в том, что игрок вынимает все камни из любой лунки ближнего к нему ряда и последовательно против часовой стрелки раскидывает их по одному в каждую лунку. Далее оставшиеся камни раскладывают в накопитель - калах и лунки противоположного ряда. В калах соперника камень не кладется.
Если последний камень попадает в калах, то игрок получает право на продолжение хода. В течение игры партнеры могут проводить таким образом серии ходов, и счет в накопителях может меняться сразу на 2, 3 или 4. Кто из игроков перенесет в свой калах больше камушков (>36 в данной игре), тот и выигрывал.
Если же последний камень попадает в пустую лунку своего ряда, а в лунке соперника напротив нее есть камни, то они становятся добычей, захватываются и переносятся в свой накопитель.
Игра длится до тех пор, пока все камни не будут перенесены в калах. Когда у одного из игроков не останется камней в своем ряду, его соперник все оставшиеся камни переносит в свой калах.
В 1971 году в журнале "Наука и жизнь” №12 сотрудники Ленинградского Университета А.А.Аникеич и Г.Г.Григорьев ознакомили читателей с этой игрой в статье "Машины играют в калах”. Статья посвящена работе первой компьютерной программы, играющей в калах. В статье есть вставка по истории игры, которую я привожу без коментариев:
 "В настоящее время одна из древних досок калаха в виде причудливой лодочки, нагруженной маленькими камешками, стоит на музейной полке в шотландском городе Абердине, в Этнографическом музее одного из местных колледжей. Подобные доски встречались в самых различных районах Азии и Африки. Они из разных материалов: вырезанные из глины, выточенные из слоновой кости, высеченные из камня. Характерное изображение двух рядов противостоящих лунок - по шесть в калах - встречается на египетских саркофагах, на ступенях афинских храмов, на каменных стеллах у обочин древних караванных путей. Эта глубоко вошедшая в жизнь народов Востока игра в средние века была предана забвению и вновь возрождена в конце XIX века. Этому способствовала выставка в г. Чикаго в 1893 г., на одном из стендов которой приводились содержание и правила игры, вызвавшие большой интерес у посетителей. В 1940 году один из американских любителей игр, Вильям Чемпион, наладил производство наборов для игры, и с его легкой руки забытая игра стала в Америке одной из популярнейших. Он же дал ей современное название "калах” от названия пустыни Калахари, где в эту игру якобы до сих пор играют местные жители”. Древняя африканская игра оказалась одной из первых игр, в которые компьютеры научились играть лучше людей. Это случилось уже в начале 1970-х годов. В шахматах ситуация переломилась только к концу двадцатого века. Теперь, чтобы попробовать свои силы в калах, можно выбрать компьютерную программу в интернете на развлекательных игровых сайтах
"В настоящее время одна из древних досок калаха в виде причудливой лодочки, нагруженной маленькими камешками, стоит на музейной полке в шотландском городе Абердине, в Этнографическом музее одного из местных колледжей. Подобные доски встречались в самых различных районах Азии и Африки. Они из разных материалов: вырезанные из глины, выточенные из слоновой кости, высеченные из камня. Характерное изображение двух рядов противостоящих лунок - по шесть в калах - встречается на египетских саркофагах, на ступенях афинских храмов, на каменных стеллах у обочин древних караванных путей. Эта глубоко вошедшая в жизнь народов Востока игра в средние века была предана забвению и вновь возрождена в конце XIX века. Этому способствовала выставка в г. Чикаго в 1893 г., на одном из стендов которой приводились содержание и правила игры, вызвавшие большой интерес у посетителей. В 1940 году один из американских любителей игр, Вильям Чемпион, наладил производство наборов для игры, и с его легкой руки забытая игра стала в Америке одной из популярнейших. Он же дал ей современное название "калах” от названия пустыни Калахари, где в эту игру якобы до сих пор играют местные жители”. Древняя африканская игра оказалась одной из первых игр, в которые компьютеры научились играть лучше людей. Это случилось уже в начале 1970-х годов. В шахматах ситуация переломилась только к концу двадцатого века. Теперь, чтобы попробовать свои силы в калах, можно выбрать компьютерную программу в интернете на развлекательных игровых сайтах
Удивительно, что историки математики не связали между собой два важных для истории цивилизаций факта. Первый, появление игр счетного характера: чисоло, вари, манкала, тогыз-кумалак (я назвал эти игры в таком порядке из-за увеличения числа камушков в лунке, соответственно: 3,4,6,9). Второй, появление у разных цивилизаций разных систем счисления - четверичной, двадцатеричной, шестидесятеричной и десятичной. В играх переноса: авари, манкале, паллангули, тогыз-кумалаке увеличивалось соответственно и число пар противолежащих лунок: 5, 6, 7, 9 .
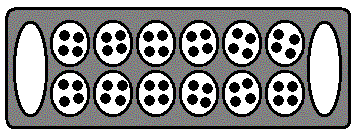 Коротко расскажу об устройстве доски и правилах вари. В исходном расположении на доске имеются два ряда противолежащих лунок, по краям - накопители. Доска во всем аналогична калаху, но набор камней другой. По 4 камня в каждой из 12 лунок, а всего - 48. Очередь первого хода определяется по жребию, а затем ходы делаются поочередно. Чтобы сделать ход, игрок вынимает все камушки (на первом ходу их 4) из произвольно выбранной лунки ближнего ряда и раскладывает по одному камушку в каждую последующую по направлению противоположному движению часовой стрелки. Дойдя до крайней правой лунки, игрок не опускает камень в свой накопитель, а продолжает ход по лункам противоположной стороны. Иногда в лунке, с которой начался ход, больше 11 камней и тогда игрок, достигнув исходной лунки, пропускает ее.
Коротко расскажу об устройстве доски и правилах вари. В исходном расположении на доске имеются два ряда противолежащих лунок, по краям - накопители. Доска во всем аналогична калаху, но набор камней другой. По 4 камня в каждой из 12 лунок, а всего - 48. Очередь первого хода определяется по жребию, а затем ходы делаются поочередно. Чтобы сделать ход, игрок вынимает все камушки (на первом ходу их 4) из произвольно выбранной лунки ближнего ряда и раскладывает по одному камушку в каждую последующую по направлению противоположному движению часовой стрелки. Дойдя до крайней правой лунки, игрок не опускает камень в свой накопитель, а продолжает ход по лункам противоположной стороны. Иногда в лунке, с которой начался ход, больше 11 камней и тогда игрок, достигнув исходной лунки, пропускает ее.
В том случае, если ход заканчивается на одной из лунок соперника и в этой последней лунке оказывается 2 или 3 камня, то игрок забирает все камни в свой накопитель. Он также забирает камни из соседних лунок соперника, если в каждой из них находится 2 или 3 камня.
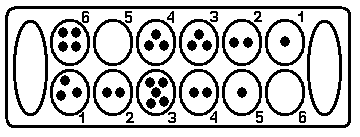 На рисунке пример эндшпиля вари: (первый игрок владеет лунками нижнего ряда). При ходе первого игрока из 3-й лунки пятый камень попадает во 2 лунку соперника, в которой оказывается 3 камня, и они переносятся в накопитель, но к этой лунке примыкают последовательно 3-я (три камня), 4-я (три камня) и 1-я лунка (2 камня). По правилам вари первый игрок забирает все камни из этих лунок. У второго игрока остается единственный ход из 6-ой лунки. Последний камень попадает в 4-ую лунку первого игрока, в которой оказывается четыре камня. Первый игрок совершает выжидательный ход из 2-ой лунки. Из-за того, что у соперника не остается в лунках ни одного камня, игра заканчивается, и все камни из лунок ближнего ряда перекладываются в накопитель 1-го игрока. Таким образом, этот игрок получает 26 камней. Для победы в игре вари игрок должен положить в накопитель 25 или более камней. Игра длится до тех пор, пока все камни не будут перенесены в накопитель или у одного из игроков в лунках не останется камней.
На рисунке пример эндшпиля вари: (первый игрок владеет лунками нижнего ряда). При ходе первого игрока из 3-й лунки пятый камень попадает во 2 лунку соперника, в которой оказывается 3 камня, и они переносятся в накопитель, но к этой лунке примыкают последовательно 3-я (три камня), 4-я (три камня) и 1-я лунка (2 камня). По правилам вари первый игрок забирает все камни из этих лунок. У второго игрока остается единственный ход из 6-ой лунки. Последний камень попадает в 4-ую лунку первого игрока, в которой оказывается четыре камня. Первый игрок совершает выжидательный ход из 2-ой лунки. Из-за того, что у соперника не остается в лунках ни одного камня, игра заканчивается, и все камни из лунок ближнего ряда перекладываются в накопитель 1-го игрока. Таким образом, этот игрок получает 26 камней. Для победы в игре вари игрок должен положить в накопитель 25 или более камней. Игра длится до тех пор, пока все камни не будут перенесены в накопитель или у одного из игроков в лунках не останется камней.
Использование камушков для счета имеет историю в десятки тысяч лет. Конечно же, этот вид счета так или иначе всегда был связан с пальцевым счетом. Интересен пример использования точек вместо камушков для обозначения объема на глиняных сосудах из Урарту. (Из книги "Культура Востока. Древность и раннее средневековье.” стр.100-104). Использовался следующий прием: для четвертей - были обозначения в виде угла вершиной вверх, дуги с выпуклостью вниз, для целых - одна точка, для девяти - одна точка в кружке.
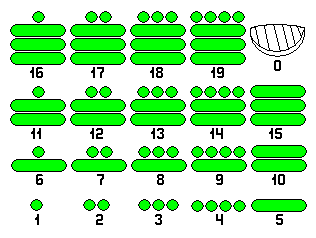 Исследователи древних культур Мезоамерики дешифровали письменность майя и их арифметическую систему счисления - двадцатеричную по существу. В этой системе у майя велось два календаря (один солнечный - 365 дней, другой ритуальный - 260 дней), поэтому осталось много документальных подтверждений. Для обозначения всех чисел использовалось всего три изображения: точка (камушек), черта (палочка) и стилизованное изображение раковины. Комбинации этих трех элементов создавали идеограмму любого числа в двадцатеричной системе (5×4). Раковина показывала отсутствие значения в разряде, т.е. являлась аналогом ноля в десятичной системе.
Исследователи древних культур Мезоамерики дешифровали письменность майя и их арифметическую систему счисления - двадцатеричную по существу. В этой системе у майя велось два календаря (один солнечный - 365 дней, другой ритуальный - 260 дней), поэтому осталось много документальных подтверждений. Для обозначения всех чисел использовалось всего три изображения: точка (камушек), черта (палочка) и стилизованное изображение раковины. Комбинации этих трех элементов создавали идеограмму любого числа в двадцатеричной системе (5×4). Раковина показывала отсутствие значения в разряде, т.е. являлась аналогом ноля в десятичной системе.
Единица обозначалась точкой (одним камушком), двойка - двумя точками (двумя камушками), тройка - тремя точками, четверка - четырьмя точками. Пятерка обозначалась уже не пятью точками, а чертой (палочкой). Шестерка - это точка и черта (1 + 5), семерка - это две точки и черта (2 + 5)... Десятка обозначалась двумя чертами, пятнадцать - тремя чертами. Девятнадцать - это четыре точки и три черты.
Следующее значение - число 20 - обозначалось снова камушком или точкой. В отличие от ассиро-вавилонской математики, где клинописные черты и разряды располагались горизонтально, майя изображали числа вертикальной идеограммой снизу вверх. Точка внизу - это единица, точка в следующей позиции выше - 20 , в третьей позиции - 400, в четвертой - 8000, в пятой - 160000 и так далее. Любая идеограмма в следующем кверху разряде увеличивала свое значение в 20 раз. Но, если майя использовали для счета камушки и палочки, древние китайцы – только палочки, то шумеры и ассирийцы обходились только камушками (или глиняными шариками, или раковинами каури, что более вероятно).
Еще до появления шестидесятеричной системы шумеры пользовались той же системой, что и майя. При дешифровке шумерского языка оказалось, что "семь” (имин) звучит как 5 + 2 (5 = иа + 2 = мин ), а девять ( иллиму ) - как 5 + 4 (5 = иа + 4 = лимму ) ("История математики”, т.1-й, изд. ”Наука” М.1970 стр.11)
Рудименты двадцатеричной системы сохраняются во многих языках мира. "Во французском языке: 70 называется soixante - dix(60 + 10), 80 - quatre - vingt (4 * 20), 90 - quatre - vingt- dix (4×20 + 10), т.е. начиная с 70, французы считают не десятками, а двадцатками. Более последовательно счет двадцатками приведен в грузинском языке, где 10 - ати, 20 - оци, 30 - оцдаати (20 + 10), 40 - ормоци (2×20), 50 - ормоцдаати (2×20 + 10), 60 - самоци (3×20) и т.д.” ("История математики”, т.1-й)
Использование для счета внутри разрядов однородного материала в виде камушков (или шариков) послужило предпосылкой к появлению вари и аналогичных игр переноса. Для уравнивания шансов игроков в начальной позиции на доске количество шариков в лунках обоих рядов выравнивалось до четырех. Право первого хода решалось по согласию или по жребию. Пример такой жеребьевки описывает А. Бэшем в своей книге "Чудо, которым была Индия”: "Слово "акша” в тексте, связанном с игрой, обычно неточно переводят "игральная кость”, но акши в самых ранних азартных играх были не костями, а маленькими твердыми орешками, называемыми "вибхишака” или "вибхидака”; очевидно, игрок вынимал горсть таких орешков из чаши, и, если число их было кратным четырем, то он выигрывал. Позднее вошли в обиход продолговатые кости с четырьмя мечеными сторонами... Игра в кости составляла хотя и небольшую, но весьма важную часть ритуала помазания царя, и помещение для игры в кости при царском дворе имело некое магическое или религиозное значение, не вполне, впрочем, нам понятное. Среди высших сановников страны, которые во время помазания царя приносили своего рода присягу на верность, был акшавапа - "бросатель” орехов или костей, очевидно устроитель игры в кости при царском дворе”.
Орехи с дерева вибхидаки использовались, по-видимому, и для игр переноса, и для игр нардового типа. В гимне игрока из "Ригведы” описывается пагубный азарт игрока, и упоминаются орехи и тенёта ореховые.
- Отрывок (перевод Т. Елизаренковой)
- Дрожащие орехи с огромного дерева пьянят меня.
- Ураганом рождённые, перекатываются по желобку.
- Словно сомы напиток с Муджават-горы,
- Мне предстояла бодрствующая игральная кость.
- …
- Ведь кости усеяны колючками и крючками.
- Они порабощают, они мучают, испепеляют,
- Одаряют, как ребёнок, победителя они вновь лишают победы.
- Но неистовство игрока обмазывает их мёдом.
- Резвиться стая их, трикраты пятидесяти,
- Законы их непреложны, как закон Савитара.
- Не уступают они наимощному в ярости,
- Даже царь перед ними в поклоне склоняется.
- Они катятся вниз, они вверх прядают,
- Без рук одолевают имеющего руки,
- Неземные угли, брошенные в желобок,-
- Сжигают сердце, хоть и сами холодные.”
Количество орехов, упоминаемое в гимне игрока для азартной игры: стая их, трикраты пятидесяти - это или 3*50, или 150 орехов. На примере игры вари видно, что и менее 50 орехов достаточно для организации полноценной игры переноса. Набор камней в играх переноса меняется в зависимости от количества камней в лунке и количества лунок. Роберт Белл приводит в своей книге (R. Bell "Board and table games from many civilizations”) наблюдения Ричарда Джобсона за игрой вари на территории Гамбии в 17 веке, когда игра в лунках велась с использованием примерно тридцати окатышей.
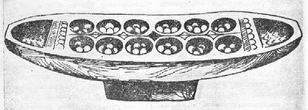 При раскопках древнейших городов долины Инда была найдена доска с возрастом более 4500 лет, в которой применялись круглые камешки и бобы. Об этой находке английский археолог Э. Маккей пишет, что "все устройство в высшей степени напоминает игральную доску, распространенную в различных африканских племенах”.(Э. Маккей "Древнейшая культура долин Инда”, М., изд. Иностр. лит.,1951, с.123)
При раскопках древнейших городов долины Инда была найдена доска с возрастом более 4500 лет, в которой применялись круглые камешки и бобы. Об этой находке английский археолог Э. Маккей пишет, что "все устройство в высшей степени напоминает игральную доску, распространенную в различных африканских племенах”.(Э. Маккей "Древнейшая культура долин Инда”, М., изд. Иностр. лит.,1951, с.123)
- Первое —это старинная легенда о награде изобретателю шахматной игры (чатуранги).
- Второе —в общности философских и игровых идей нескольких четверных индийских игр, включая чатурангу, игру переноса "рума” (смотрите ниже - Буддийская "колесница" в индийских играх), игры нардового типа "чупур” и "тааям”, а также игру шашечного типа, на доске которой в Шри-Ланке и Индии дети играют "Леопард и стадо”, в Тибете - в игру "Два монаха”.