 |
Древность шахматных игр |
|
|
Чатуранга в трактате аль-Бируни
В завершенном в 1030 году труде «Индия, или Книга, содержащая разъяснение принадлежащих индийцам учений, приемлемых разумом или отвергаемых» аль-Бируни дал детальное научно-критическое описание быта, культуры и науки индийцев, изложил их религиозно-философские системы, достаточно точно переложив учение классической санкхьи, теорию космической эволюции, учение о связи души с «тонким телом» и др. Здесь же изложена знаменитая легенда о создателе игры в шахматы. В трактате аль-Бируни "Индия" приведено описание индийской шахматной игры для четырёх игроков. Анализ текста позволяет сделать важные выводы для истории шахмат. Была ли древнеиндийская Чатуранга медленной и неинтересной, игралась ли она только на полное истребление всех фигур? Из этнографического описания этой игры, сделанного на основе личных впечатлений знаменитым хорезмийским ученым Бируни в труде "Индия" (начало XI в.), можно увидеть, что чатуранга ещё сильно отличалась от нынешней игры: фигуры располагались в четырёх углах доски, не было ферзя. По первому впечатлению, четыре игрока могли бы вести борьбу до полного уничтожения фигур. Их ходы определялись показаниями костей, и этот элемент случайности придавал игре азартный характер. Казалось бы, Чатуранга мало чем отличается от многочисленных игр в кости, которые издавна были известны в Индии. Но это не так! Древнеиндийская Чатуранга, попав в Иран и Китай, оторвалась от буддийской основы, но не потеряла привлекательности для других народов. Известно, что по распоряжению Хосрова I Аношрована (год рождения 509, годы правления 531-579) иранский лекарь Борзуйа совершил поездку в Индию, откуда в Джонди-Шапур привез книгу "Калила и Димна", интеллектуальную игру - шахматы, некоторые книги по медицине, а также нескольких индийских врачей. (Хосейнали Момтахэн. История Джонди-Шапура. Ах-ваз, университет Джонди-Шапур, 1347 (1968), с. 35.) О том, что Хосров I был очарован индийской игрой, свидетельствует проведённая им военная реформа. Вот этот красноречивый факт. Хосров I упразднил должность единственного и главного военночальника Ирана (Эранспахпата) и вместо него ввёл четырёх спахпатов, то есть военначальников армий четырёх частей государства, соответствующих четырём частям света. Спахпат юга командовал войсками Хузистана и Пасрса, спахпат Запада — войсками Ирака, спахпат севера — армиями Азербайджана и Мидии, спахпат востока — войсками Хоросана, Сакастана и Кермана. О том, что Чатуранга попала в Иран во время правления Хосрова I, свидетельствует текст Матикан-и-чатранг (Книга о чатранге). Книга была переведена с пехлевийского языка в 1886 году русским академиком К.Г. Залеманом. В знаменитом трактате о настольных играх, написанном в 1283 году в Севилье по повелению кастильского короля Альфонса X Мудрого [рукопись хранится в Эскуриале], приводится легенда об изобретении шахмат, костей и нарда. Легенда находится в предисловии, написанном от лица самого дона Альфонса. И по этой легенде шахматы были изобретены в Индии. Вот упоминания о Чатуранге в индийских источниках: В поэме Субандху "Васабадата”, написанной в конце VI в. н.э., встречаются такие строки: "Сезон дождей разыграл шахматную партию, используя в качестве фигур желтых и зеленых лягушек, прыгавших на разноцветные поля садовых клумб”. В поэме Бани "Хартахарита” воспевались миролюбие и гуманность царя Каньякутджи - Шри-Харши. По словам поэта, в период правления этого просвещенного государя "не происходило никаких других распрей, кроме распрей между собирающими мед пчелами, не отрезали других стоп, кроме стихотворных, не вводили в действие никакие другие армии, кроме армий 64 клеток шахматной доски (аштапады)”. Удивительно, но факт: описание древней игры на санскрите встречается в индийских источниках только в XVI в. - у Рагхунанды, автора, жившего во II-й половине XVI в., под названием caturaji ("игра четырех королей"). Для шахматных историков очень важно описание чатуранги, сделанное выдающимся ученым-энциклопедистом аль-Бируни в трактате "Путешествие в Индию”, написанном на арабском языке в 1031 г. Полное имя ученого из Хорезма Абу Рейхан Мухаммед аль-Бируни (973-ок.1050 гг.). Его труды по математике и астрономии вызывают восхищение даже современных ученых. Аль-Бируни первым в Средней Азии высказал идею о вращении Земли вокруг Солнца. Аль-Бируни отлично знал правила шатранджа и при описании индийской игры сравнивал последнюю именно с шатранджем. "Языческая" индийская чатуранга описана скупо. Бируни, как искренний приверженец ислама, не стремился раскрыть необычный философский подтекст игры и остановился на внешней стороне - на конкретных правилах. Ниже приводится перевод из книги Бируни "Индия" (1995 г.; Научно-изд. центр "Ладомир", стр.186-187. Глава XVI, в которой излагаются сведения об индийском письме, арифметике и тому подобных преметах и некоторых индийских традициях, которые могут показаться диковинными). При переводе в текст книги для облегчения восприятия были вставлены современные шахматные термины: байдак - пешка, рух - ладья, фарас - конь, фил - слон, шах - король. "На шахматном поле они передвигают фила (слона) вперед, но не в другие стороны (прямые), на одну клетку [в один ход], как пешку, и по диагонали [по направлению] ко всем четырем углам на одну клетку [в один ход], подобно фирзану [ферзю]. Они говорят, что эти [пять] клеток суть места его [пяти] конечностей - хобота и четырех ног. У них играют в шахматы двумя комплектами четыре человека одновременно. Что же касается расстановки фигур на доске, то вот ее схема:
По той причине, что этот вид шахмат у нас неизвестен, я расскажу то, что о нем знаю. Дело в том, что четверо играющих в шахматы усаживаются вокруг доски по четырем углам и по очереди ходят фигурами то одного, то другого комплекта. Из порядковых номеров комплекта пять и шесть считаются недействительными, и вместо пяти берут единицу, а вместо шести - четыре, потому что в изображении эти два числа будут выглядеть таким образом: 6 5 4 3 2 1 Каждый порядковый номер комплекта служит [поводом] для продвижения одной из фигур. Число один [1] - для хода пешки или короля, которые передвигаются как в обычных шахматах; король может быть взят, но не обязательно должен покидать свое место. Число два [2] - для хода ладьи, которая ходит до третьей клетки по диагонали, как слон в наших шахматах. Число три [3] - для хода коня, который ходит как обычно на третью клетку, отклоняясь [на одну клетку] в сторону. Число четыре [4] - для хода слона, который передвигается по прямой линии, как ладья в обычных шахматах, если только нет препятствия на пути его передвижения. Часто такое препятствие бывает, и тогда один из комплектов устраняет препятствие, чтобы он мог передвигаться. Наименьший из [возможных] его ходов - на одну клетку, а наибольший - на пятнадцать, потому что часто в обоих комплектах встречается либо две четверки, либо две шестерки, либо шестерка и четверка. При одном из этих числе слон передвигается во всю длину одного края шахматного поля, а при другом числе он передвигается во всю длину другого края шахматного поля, если на его пути нет препятствия. При обоих числах слон может занять клетки на обоих концах диагонали. Каждая фигура имеет [определенную] стоимость, согласно которой они получают доли ставки, потому что фигуры берутся и остаются в руках [игроков]. Стоимость короля - три, ладьи - два и пешки - один. Игрок, выигравший короля, получает пять, за двух королей - десять, за трех королей - пятнадцать, если у выигравшего нет своего короля. А если он сохранил своего короля и завладел тремя королями, то он получает пятьдесят четыре - это есть число [установленное] по взаимному согласию, а не по законам арифметики". О ставках в игре и "мате".Действительно, появление числа 54 было непонятным для Бируни. Если стоимость одного шаха (короля) - 5, двух - 10, трёх - 15, то логично было бы за трёх шахов (королей) при сохранении своего (всего 4) дать 20 долей ставки. Для объяснения числа 54 необходимо подсчитать первоначальную долю выигравшего игрока. В начале игры: 5(король)+4(слон)+3(конь)+2(ладья)+1х4(пешки)=18 Доли остальных трех игроков: 18 х 3=54 Можно сделать заключение, что выигрыш трех королей при сохранении своего приравнивается к выигрышу начальных долей ставки трех других игроков. Всего ставок в игре: 18 х 4=72, но 18 из них ставки - это ставки самого игрока и они возвращаются, а не выигрываются. Юрий Авербах написал так: (в статье "О происхождении шахмат") "Вопреки аль-Бируни, в точном соответствии с законами арифметики. Первым, кто поправил аль-Бируни, был Мэррей, но он не сделал следующего шага. А для нашей гипотезы этот шаг чрезвычайно важен. Ясно, что 54 очка - это победа: у игрока в руках все три шаха противника. Но тогда, рассуждая логично, для победы в игре для двоих достаточно забрать только одного неприятельского короля - иначе говоря, дать ему мат. И мы приходим к выводу, что идея мата - король получил мат - игра проиграна, автоматически возникает при трансформации игры для четверых в игру для двоих." В тексте рукописи рисунок доски сделан с надписями названий фигур красными и чёрными чернилами так, что названия фигур с противоположных по диагонали сторон сделан одним цветом. Учитывая древние традиции парных игр Индии можно думать о том, что аль-Бируни видел именно набор фигур для парной игры (иначе он бы просто подписал, что армии каждого игрока обозначаются для отличия от армий других своим цветом- красный, жёлтый и т. д.) При парной игре для выигрыша достаточно выиграть двух королей (при сохранении двух своих). При дальнейшей трансформации парной игры в игру для двоих - достаточно выиграть одного короля. Таким образом, можно считать, что идея мата (то есть выигрыш короля=выигрыш партии) уже был в индийской игре. И не надо для выигрыша истреблять весь комплект фигур противников! Итак, игрок максимально может взять в плен три армии (стоимостью в 54 доли) или взять трех королей, сохраняя своего короля (стоимостью 54 доли). Гипотетически - сделав и то, и другое, игрок получает 54+54=108!!! Это же число -108 мы уже встречали: (Движение на аштападе) В Ведической астрологии, зодиак подразделен на 27 накшатр. Каждая накшатра подразделена на 4 четверти. ( 27 * 4= 108) Магическое число 108 - это число, имеющее свои атрибуты в современном буддизме: 108 зерен в четках, которые придумали буддийские монахи для подсчета молитв. 108 барабанов-цилиндров окружают храм буддийского монастыря /дацана/, а вращение этих барабанов символизирует прочтение молитв, освобождающих от 108 известных болезней. Богомольцы прежде чем войти внутрь храма, приводят в движение один за другим 108 молитвенных барабанов. "Можно говорить о чем угодно и с кем угодно на языке знания, но лишь с единоверцем можно беседовать на языке веры," - эти слова писателя Еремея Парнова объясняют причину непонимания Аль-Бируни языческой символики. Сакральное число 108 унаследовано буддистами от брахманистов. До сих пор в Непале на празднике в честь Дурги (жены бога-разрушителя Шивы) приносят в жертву 108 буйволов. Е.Парнов в своей книге "Боги лотоса" приводит интерпретацию магического числа 108: "В индийской, как и в других культурах Востока, алфавит и числовой ряд помимо основной роли несли и тайную эзотерическую нагрузку. На языке посвященных ноль означал еще пустоту, небо, отверстие, бесконечность; единица (эка) - начало, Луну, Землю, тело, предка, брахмана ; двойка (дви) - близнецов, ноздри, глаза, Солнце в паре с Луной; тройка (три) - огонь, драгоценность, Шиву (трехглазый), три мира, три времени (прошлое, настоящее, будущее) и т.д. Теперь, вооруженные основами тайных знаний, доступных некогда лишь брахманам, попробуем разложить вездесущее число на простые множители: 108=1х2х2х3х3х3 Полученный результат можно представить в виде так называемого магического треугольника".
1 Начало (Брахман) Брахма 2 2 Солнце Луна 3 3 3 Прошлое Настоящее Будущее
Основа магического треугольника числа 108 - всепожирающее время, которое индуисты чтут под именем Кала Бхайрава, буддисты поклоняются как Махакале (Великому Времени). Разрушающему началу Махакалы (Шива) противостоит созидающий Брахма (Вишну). Одни пожирает время, другой ткет его. В эпосе "Махабхарата" есть миф о том, как два бога - Солнце и Сома ("месяц") своей животворящей силой породили растения : "Воистину пища всех наделенных жизнью существ сотворена из Солнца, а поскольку оно и есть отец всех существ, моли его о помощи, называя одним из ста восьми святых его имен". Далее в тексте "Махабхараты" называются 108 имен, выражающих проявление солнечного бога-творца: Сурья, Тваштар, Пушан, Савитар, Индра, Пламя чрева, Яма и т.д. Мастер, создавший игру чатуранга, разделил доску для четырех участников. Но ведь и Брахма разделил мир между владыками четырех сторон света: Индре достался Восток, благодатный край, первым открывающийся свету. Восток охраняется белым слоном Айраватой, главным из четырех мировых слонов, которые мягко держат землю. Яме достался Юг. Царство Ямы опирается на голову слона Махаладмы. Варуна владеет Западом. Слон Варуны Вамана стережет Запад. Севером владеет Кубера (бог богатства), любимец Брахмы. Таковы владыки четырех частей света, назначенные Брахмой, чтобы охранять мир. В иконографии Наставника мира - Брахму - изображали как бородатого мужа с четырьмя телами, четырьмя лицами и восемью руками. Лица Брахмы обращены к четырём сторонам света... Об использовании игральных костей в индийской игре.В индийской игре произошло качественное изменение в использовании костей. Во всех азартных играх нардового типа по сумме очков на зарах (игральных костях) определяют длину хода фишки. В Чатуранге же определяется не длина хода! Определяется фигура, которой игрок может ходить - при этом он может делать выбор из нескольких траекторий (например, конь в в центре доски может встать на одну из восьми клеток). Надо признать, что по мере уменьшения фигур на доске, броски костей становятся всё менее результативными в плане выигрыша. Вместо выигрывающего хода слоном (или конём), выпадает ход другой фигурой. Это растягивает игру во времени и наводит на мысль, что кости вовсе не нужны. Когда в этой парной игре вместо 4 игроков участвуют 2 игрока, то эта мысль ломится буквально в открытую дверь. Игроки и так ходят по очереди фигурами удвоенного комплекта. При выпадении на костях хода пешкой - какой пешкой (какого комплекта) надо ходить, если все фигуры удвоенного комплекта принадлежат одному игроку. О ходе слона. О динамизме игры в Чатурангу.На шахматных сайтах часто высказывают такое мнение: Органический недостаток шатранджа — недостаток динамизма, особенно в дебюте, вызванный слабостью унаследованных от Чатуранги фигур. Так ли это?
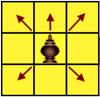
Слону из Чатуранги доступна вся доска! "Кроме клеток по диагонали ему ещё доступен шаг вперёд. На шахматном поле они передвигают слона вперед, но не в другие стороны, на одну клетку [в один ход], как пешку, и по диагонали [по направлению] ко всем четырем углам на одну клетку [в один ход], подобно ферзю. Они говорят, что эти [пять] клеток суть места его [пяти] конечностей - хобота и четырех ног." Сделал слон шаг вперёд и поменял диагонали, по которым он может двигаться. Когда индийские игроки отказались от бросания костей, то длина хода слона сократилась до хода, показанного на рисунке. Это и есть суть хода слона, соответствующая местам его [пяти] конечностей - хобота и четырех ног. Именно такое понимание хода слона унаследовано из первых рук наследниками Чатуранги в Мьянме и Таиланде. Ведь там это понимание пришло на фоне общего индийского культурного влияния и без религиозного барьера (В Таиланд из Индии пришёл буддизм, а письменность - на основе санскрита). Смотрите правила хода слона в таких играх, как Макрук (Таиланд), Ситтуйин (Мьянма), Оу (Камбоджа). Родоначальники шатранга (Иран) эту суть не уловили, поэтому ход ладьи приписали слону. В шатранге (а затем и в арабском шатрандже) слон стал ходить по диагонали на третью клетку! Это и привело в дальнейшем к появлению разнопольных слонов в шахматах. Можно сделать вывод, что отказ от костей лишил динамизма игры-последователи Чатуранги. В последующем в шахматах были приняты правила рокировки, двойного движения пешки на её первом ходу, увеличение дистанции хода слонов и ферзя, но эти правила были применены для усовершенствования шатранджа! Анализируя текст оригинала (совместно с А.Б. Халидовым), И. Линдер обратил внимание на следующие особенности: "Как видно из приведённого текста, названия фигур и игры обозначены Бируни не санскритскими словами, а персидско-арабскими. Отсюда можно сделать вывод, что при описании игры автор не пользовался литературными индийскими источниками, а собственными наблюдениями. К тому же, он, по-видимому, не делал записей, наблюдая за игрой. Да и в своём описании Бируни не ставил задачу дать всестороннее представление о чатуранге, а ограничился лишь некоторыми штрихами, которые могли бы отразить её специфику. Может быть, этим объясняются встречающиеся у автора отдельные противоречия, в частности, в описании хода слона. Если вначале Бируни рассказывает о "пятистопном" ходе слона, который был известен только в Индии, то в конце отрывка ход этой фигуры описывается уже в том виде, как он применялся в игре для двух соперников (шатранге). Судя по всему, этот вид игры тоже был распространён в то время в Индии (самый северо-запад и территория нынешнего Пакистана, только там где Бируни реально был. В центральную Индию он не попадал), но со своими особенностями. В частности, слон ходил как рух (ладья), а рух передвигалась подобно слону в шатрандже. В пользу того, что Бируни наблюдал в Индии обе игры - и для четырёх и для двух противников, - говорит по мнению известного английского историка Г. Мэррея, и курьёзное приравнивание в описываемой игре обозначений короля и ферзя, хотя последнего в чатуранге не было." Однако, следование точному переводу текста Бируни исключает кажущееся противоречие в ходе слона. 1. Ход слона (в индийской игре) как пешкой - это минимальный ход на следующую вперёд клетку, а не в других ортогональных направлениях. Число четыре [4] - для хода слона, который передвигается по прямой линии, как ладья в обычных шахматах (шатрандже)... - а это ход по прямой линии от себя при максимальном ходе. 2. Ход слона (в индийской игре) по диагонали [по направлению] ко всем четырем углам на одну клетку [в один ход], подобно фирзану [ферзю] - это минимальный ход на соседнюю клетку по диагонали. В шатрандже так ходит ферзь! Наименьший из [возможных] его ходов - на одну клетку, а наибольший - на пятнадцать, потому что часто в обоих комплектах встречается либо две четверки, либо две шестерки, либо шестерка и четверка. При одном из этих числе слон передвигается во всю длину одного края шахматного поля, а при другом числе он передвигается во всю длину другого края шахматного поля, если на его пути нет препятствия. При обоих числах слон может занять клетки на обоих концах диагонали. Это описание максимального хода индийского слона по диагональным направлениям в Чатуранге. Никакого противоречия на самом деле нет, так как длина хода слона в Чатуранге зависела от пары костей. Первая кость="четвёрка" определяла фигуру, то есть ход слона. Вторая кость="единица", определяет ход слона как "суть места его [пяти] конечностей - хобота и четырех ног". Если вторая кость показывает другие значения, то меняется только длина хода, но по тем же пяти направлениям! Бируни точен в расстановке на доске фигур слона (Фил в шатрандже) и ладьи (Рух в шатрандже). Путаница в расстановке этих фигур (по других источникам) связана с прямым ходом слона, который аналогичен ходу шахматной ладьи вперёд из начальной расстановки фигур. Не смотря на использование костей в игре, Чатуранга давала игрокам необычный выбор для размышлений. Даже при детерминированном ходе определённой фигурой, игрок имел широкий выбор направлений хода. Даже при минимальной длине хода: конь мог ходить на одно из 8 полей, слон на одно из пяти, ладья - на одно из 4. И только пешка - на одну клетку, но-!- даже здесь игрок имел выбор, какой из 4 пешек (или же королём) совершить этот ход. При этом король имел 8 направлений хода. |
Аль-Бируни, великий учёный из Хорезма, получил широкое математическое и философское образование. Его учителем в древней столице хорезмшахов Кяте был выдающийся математик и астроном Ибн Ирак. После взятия в 995 году Кята эмиром Гурганджа и переноса столицы Хорезма в Гургандж аль-Бируни уехал в Рей, где работал у ал-Ходжанди. Затем он работал в Гургане при дворе Шамс аль-Ма’али Кабуса, которому он около 1000 года посвятил «Хронологию», затем вернулся в Хорезм и работал в Гургандже при дворе хорезмшахов Али (997—1009) и Мамуна II. С 1017 года, после завоевания Хорезма султаном Махмудом Газневи он был вынужден переехать в Газну, где работал при дворе султана Махмуда и его преемников Масуда и Маудуда. Аль-Бируни участвовал в походах Махмуда в Индию, где прожил несколько лет.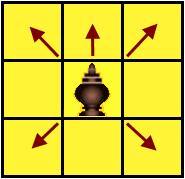
Ведь даже высказывание аль-Бируни опровергают этот тезис! Например, разберём ход слона: "На шахматном поле они передвигают слона вперед, но не в другие стороны, на одну клетку [в один ход], как пешку, и по диагонали [по направлению] ко всем четырем углам на одну клетку [в один ход], подобно ферзю. Они говорят, что эти [пять] клеток суть места его [пяти] конечностей - хобота и четырех ног. ... Число четыре [4] - для хода слона, который передвигается по прямой линии, как ладья в обычных шахматах, если только нет препятствия на пути его передвижения. Часто такое препятствие бывает, и тогда один из комплектов устраняет препятствие, чтобы он мог передвигаться. Наименьший из [возможных] его ходов - на одну клетку, а наибольший - на пятнадцать, потому что часто в обоих комплектах встречается либо две четверки, либо две шестерки, либо шестерка и четверка. При одном из этих числе слон передвигается во всю длину одного края шахматного поля, а при другом числе он передвигается во всю длину другого края шахматного поля, если на его пути нет препятствия. При обоих числах слон может занять клетки на обоих концах диагонали." Видно, что динамика движения слона из Чатуранги значительно превосходит движение слона в шатрандже. Даже в современных шахматах слону доступны клетки только половины доски, поэтому слонов и различают на чернопольных и белопольных.