Есть два удивительных обстоятельства, связывающих счетные доски и игры переноса с возникновением чатуранги - родоначальницы шахмат.
- Первое —это старинная легенда о награде изобретателю шахматной игры (чатуранги).
- Второе —в общности философских и игровых идей нескольких четверных индийских игр, включая чатурангу, игру переноса "рума” (смотрите ниже - Буддийская "колесница" в индийских играх), игры нардового типа "чупур” и "тааям”, а также игру шашечного типа, на доске которой в Шри-Ланке и Индии дети играют "Леопард и стадо”, в Тибете - в игру "Два монаха”.
Легенда о награде изобретателю шахматной игры, проверка её методами древней математики.
В период арабского завоевания Ирана (7 век) появился ряд легенд об индийском происхождении шахмат. Самая известная из них об индийском царе Шераме-Шихране, который позвал к себе изобретателя шахматной игры, своего подданного Сету, чтобы наградить его за остроумную выдумку.
Давайте ознакомимся с популярной шахматной легендой и проведём её анализ с позиций индийской математики 4-5 -го века, то есть со времени реального появления этой игры. Она приводится не только в шахматной литературе, но и по праву в популярной математической литературе. В России данная легенда была впервые напечатана в журнале "Отечественные записки" 1839г. т.X, стр.12. в статье "Награда изобретателю шахматной игры". В последующем писатели передавали содержание этой статьи с незначительной разницей в деталях.
Индийский царь ознакомился с шахматами и поразился глубине идей и разнообразием событий в них. Узнав, что мудрец, придумавший эту чудесную игру, является его поданным, он решил позвать наградить его. Награда должна быть достойной властелина, а игра должна прославить не только страну, но и щедрость индийского царя. Властелин спросил мудреца,- какой награды он хочет? Изобретатель шахмат попросил зерна. Столько, сколько получится, если на первую клетку положить одно зерно, на вторую - в два раза больше, т.е. два зерна, на третью - снова в два раза больше, т.е. 4 зерна, и на каждую последующую клетку в два раза больше, чем на предыдущую, и так до 64-й клетки. Властелин приказал сосчитать и выдать положенное в награду зерно, сочтя такую награду ничтожной. Однако через некоторое время придворные математики доложили властелину, что не в состоянии выполнить просьбу мудреца, т.к. число зерен равно: 18.446.744.073.709.551.615 (!)
Надеюсь, читатель легко произнесёт вслух это двадцатизначное число зерен - 18446744073709551615 (18 квинтильонов 446 квадрильонов 744 триллиона 73 биллиона 709 миллионов 551 тысяча 615), чего мне не удалось сделать сразу. Такого количества зерна нельзя было собрать не только в амбарах властелина, но и во всем мире, и даже за всю историю человечества.
Попробуем ответить на два вопроса:
- Могли ли индийские математики назвать это число?
- Могли ли индийские математики правильно вычислить результат?
Дж. Неру в своей книге "Открытие Индии” писал: "В Индии имелось 18 специальных наименований (1018) и встречались даже более длинные перечни. В сказании о раннем периоде учения Будды говорится, что он ввел наименование чисел для 1050”. Бируни в 1030 году написал в книге "Индия”, что "названия всех разрядов счета до восемнадцатизначного числа даны в таблице:
1.Экам 7.Праюта 13.Махападва
2.Дашам 8.Коти 14.Шанку
3.Шатам 9.Ньярбуда 15.Самудра
4.Сахасрам 10.Падма 16.Мадхья
5.Аюта 11.Кхарва 17.Антья
6.Лакша 12.Никхарва 18.Парадха.
Что касается употребления чисел в арифметике (у индийцев), то оно соответствует нашим обычаям. Я составил (особый) трактат о тех больших (чем у нас) достижениях в этой области, которые, быть может, у них имеются”.Бируни в своей книге пишет, что "некоторые индийцы утверждают, будто после парарадхи имеется еще девятнадцатый разряд, называемый бхури. и будто далее нет счета. Однако счет нескончаем, лишь условно можно установить его предел, который будет одновременно концом его разрядов. Похоже на то, что в этом выражении ("далее нет счета”) речь шла не о счете, а о названиях (разрядов счета)”. Необходимо признать, что в Индии существовали длинные перечни не только для десятичных разрядов. Позднее буден приведён перечень четверичных разрядов, которые реально использовались в Др. Индии для практических целей.
Следуя индийским названиям десятичных разрядов, напишем название числа из легенды. Непривычно звучит перечисление каждого разряда, но это факт!
18 бхури 4 парадха 4 антья 6 мадхья 7 самудра 4 шанку 4 махападва (0 никхарва) 3 кхарва 7 падма 7 ньярбуда (0 коти) 9 праюта 5 лакша 5 аюта 1 сахасрам 6 шатам 1 дашам 5 экам.
Попробуем сосчитать сами число зерен. Обозначим сумму зерен через S.
S = 1+ 2+22+23+24+...+262+263.(1)
Умножим обе части записанного равенства на 2(знаменатель геометрической прогрессии) и получим:
2S= 2+22+22+23+24+...+262+263+264.(2)
Вычтем почленно из 2-го равенства первое и проведем упрощения:
2S-S=(2+22+22+23+24+...+262+263+264) - (1+2+22+23+24+...+262+263).
S = 264 - 1.
Теперь компьютер выдаст результат, который можно получить и на счетной доске с лунками путем повторных сложений. В первых веках нашей эры (что соответствует времени изобретения шахмат) индийцы могли назвать приведенное выше число и могли вычислить его при помощи досок с лунками. Названия 18 разрядов соответствуют количеству счётных лунок, традиционно использовавшихся индийскими математиками. Для подсчётов по легенде количество лунок необходимо увеличить всего лишь до двадцати. Переход к десятичному счислению не требовал новой счетной доски и значительной переделки механизма переноса камней. Каждая счётная лунка могла заполняься до 9. При попадании десятого все камни вынимались,а один переносился в лунку старшего разряда. При вычитании из лунки вынимались камни, но при их нехватке в лунку добавляли десяток камней из резерва и при этом отнимали один из лунки старшего разряда. Использование десятичной системы счисления на досках требовало лишь увеличения набора счётных камней до 9 на каждую лунку.
Итак, анализ легенды об изобретателе шахматной игры и задаче о числе зерен за 64 клетки доски свидетельствует о том, что шахматный и математический фольклор не противоречит исторической действительности. К данной легенде необходимо относиться именно как к легенде, а не как к анекдоту. В Индии в начале 1-го тысячелетия умели возводить в квадрат и складывать большие числа. Для вычислений имелась традиция использования счетных досок, и даже специальные названия для десятичных разрядов. При дворах индийских махарадж существовала должность устроителя игр, в обязанности которого входило и изобретение новых игр. Изобретатель шахмат, безусловно, был математиком, но эту точку зрения способен подтвердить лишь анализ математического каркаса индийской шахматной игры, т.е. чатуранги
Тогыз-кумалак. Казахская игра - свидетельство зарождения десятеричной системы счисления
При переходе к десятичной системе на счётных досках изменился набор камней в сторону увеличения, так как для каждой разрядной лунки необходимо 9 камней. В связи с тем, что исторически счётные доски с лунками сопровождались играми переноса,мы вправе ожидать,что и десятичную счётную доску по традиции сопровождала игра. Самое интересное в том, что такая игра не только появилась, но и жива до сих пор. Это старинная казахская игра тогыз-кумалак.
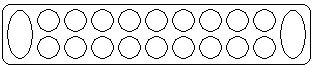"Не так давно казахстанскими археологами были сделаны интереснейшие открытия, открывающие новое в истории тогыз-кумалака. При раскопках древнего поселения периода III - IV веков н.э. (Южно-Казахстанская область) ученые обнаружили различные шарики, специально выточенные для игры. В результате тщательного исследования они пришли к выводу, что шарики служили для игры в тогыз-кумалак. В это же время в 30 км от г. Джамбула на одной из скал Бурлинских гор археологи обнаружили рисунок, изображающий доску для игры в тогыз-кумалак. На каждой стороне доски имеется по 9 лунок, т.е. столько же, сколько имеет современная доска для игры”.
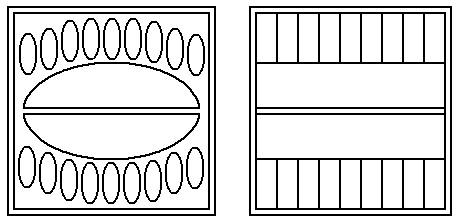Из-за увеличения количества лунок накопители (казан) стали располагать не на краю, а в центре доски, что способствовало изменению формата доски. В 20 веке Абилда Акшураев предложил модифицированную доску с прямоугольными лунками, на обратной стороне которой можно играть в шахматы. В связи с тем, что в игру тогыз-кумалак проводятся специальные соревнования и чемпионаты, игра стала спортивной на национальном уровне. Первый чемпионат Казахстана по тогыз-кумалаку был проведён в 1948 году. Победителем тогда стал Ш. Утегенов из Джамбульской области. Наиболее подробно современные правила игры приведены в книге А. Акшураева "Тогыз-кумалак”(1983 г.). Слово тогыз переводится с казахского языка: девять. Многие авторы считают, что число 9, доминирующее в игре тогыз-кумалак, считается священным у монгольских и тюркских народностей и его можно считать традиционным у казахов. Однако, если смотреть на игровую доску как на древнейшую счетную доску, то цифра 9 - символ заполнения разряда, т.к. при попадании в лунку следующего камушка все камушки из нее вынимаются и в следующую лунку кладется один камень. Казахи широко применяли десятичную систему, а счетная доска могла применяться для вычисления налогов. В земледельческих районах собирался налог "ушур”, то есть десятая часть урожая. В скотоводческих районах - налог "зякет” - одна двадцатая часть скота.
Буддийская "колесница" в индийских играх.
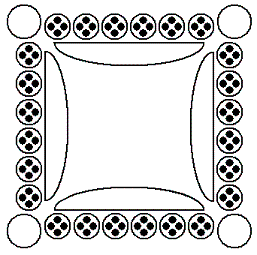Теперь обратимся к другой индийской игре, хорошо известной на территории бывшего СССР. Эта игра"Рума”. Появление этой игры, как упоминалось ранее, сопряжено с появлением чатуранги. Возможно даже, что изобретатель румы и чатуранги один и тот же человек, который был и математиком, и страстным игроком, и буддистом, и изобретателем игр. Рума представляется мне дхармачакрой - колесом судьбы. Играющих в руму можно назвать словами Николая Асеева "привязанными к колесу влачащихся дней и событий”. Одно малое колесо судьбы из 24 спиц: 4 колеса, вращающиеся в 4-х разных направлениях, замыкают еще один большой круг движения - большое колесо. У каждого игрока в руму по двадцать четыре шарика - ореха (помните: вибхидака) или раковины каури, по четыре в каждом из шести основных полей. Так как в руму играют 4 человека, то всего таких основных полей 4×6 = 24! (спицы большого колеса)
В исходном положении игры рума круглые лунки по углам доски - это накопители. Их называют румами. Оказавшиеся в румах шарики более не участвуют в игре, как и в других играх переноса. Дополнительные удлиненные лунки в центре доски - это мусорные лунки. Они также исполняют роль накопителя, но для штрафных шариков. Игроки по очереди делают ход в направлении против часовой стрелки, перенося шарики по одному в лунку сначала по своим полям. затем по основным полям противника и т.д. Ход считается возможным только в том случае, если последний шарик не попадает на пустую лунку. Ход возможен, если последний шарик попадает в рум. Если один из игроков не может совершить ход, то он перекладывает один шарик из своего накопителя - рума в мусорную лунку, а ход пропускает. Выигрывает тот, кто первый избавится от всех шариков на своей стороне доски, хотя может иметь до 11 штрафных шариков в мусорной лунке. Получивший 12 штрафных шариков выбывает из игры, поэтому может выиграть и тот игрок, у которого все три соперника выбыли из-за штрафов.
Интерпретация игры Рума
Наличие "малых колес” и "большого колеса” - указывает на буддийскую идею "колесницы”. По буддийскому учению человек остается в кругу страданий и перерождений; чтобы достичь блаженства, он должен преодолеть пропасть, разделяющую "небесный град” от грешной земли. Следование учению Будды - это и есть колесница, способная перенести через поток жизни и прервать страдания. В Индии в течение многих веков до изобретения румы сложилось представление, что "движение светил в направлении юго-восток считается подобным движению колеса. Все планеты движутся на восток и движение их едино. И такова их цель в тысячах прошлых рождений”. О том, что доска для игры так же могла использоваться для счета, можно догадаться при ознакомлении с главой "Об индийской системе мер” в книге Бируни "Индия”. Вот цитата из книги Бируни:
Что касается сухих веществ [автор - речь о мерах объема для сыпучих веществ], то для них четыре палы - [одна] кудава, четыре кудавы - [одна] прастха, четыре прастхи - [одна] адхака. Для жидкостей: восемь пал - [одна] кудава, восемь кудав - [одна] прастха, четыре прастхи - [одна] адхака, четыре адхаки - [одна] дрона",- Бируни приводит меры веса, ссылаясь на книгу "Чарака - самхиту”. Я приведу лишь часть названий, исключая ряд промежуточных мер: "Четыре анди - одна маша, четыре маша - одна шана, четыре шана - одна карша (суварна), четыре суварны - одна пала, четыре палы - одна кудава, четыре кудавы - одна прастха, четыре прастхи - одна адхака, четыре адхаки - одна дрона"...
Существование в Древней Индии разных систем мер, применение одних и тех же терминов по отношению к различным мерам - это возможно при использовании счетных досок с лунками, когда каждая лунка имеет определенное название. Тогда попадание камушка (ореха или раковины каури) в определенную лунку будет названо одним и тем же термином, несмотря на то, что подсчитываться может вес, объем сыпучих веществ, объем жидкости, расстояния, время. Например: термин "пала” в санскрите означает определенную единицу времени, равную приблизительно 24 секундам. Этот же термин "пала” применялся в Древней Индии как мера веса, как мера сыпучих тел, как мера объема жидкостей!
Итак, мы предположили, что доска Рума использовалась для расчетов. Это универсальная система счета идеально подходит для торговли. Для торговли с Румской землей, то есть с Византией. Название "Рум" на средневековом Востоке ассоциировалось с Малой Азией и Грецией и с названием Византии - "Восточной Римской империей".
Под влиянием индийской культуры, буддизма и торговли игры переноса распространялись по Юго-восточной Азии. Один комплект игры из Малайзии был подарен Государственному музею искусства народов Востока. Примечательно, что вместо круглых камушков в комплект игры джонгкак входят ракушки. В Древней Индии длительное время ракушки каури использовались в качестве денег. Эти красивые ракушки добывались у берегов Африки и доставлялись в Индию, благодаря торговле. После появления других денежных эквивалентов ракушки каури обесценились и стали использоваться для украшений и для игр на счётных досках, на тех самых, на которых эти ракушки считали за деньги. Игра из Малайзии подтверждает многовековые влияния африканской культуры (через Ирак - Иран - Индию) на удалённые страны Азии.
В Древнем Китае счетные доски с лунками не нашли применения по одной простой причине: для расчетов использовались счетные палочки! Отказ от лунок на счетной доске не означает отказ от позиционного принципа. Для распознавания разрядов счетные палочки раскладывались на доске в двух направлениях. Об этом методе написал китайский математик третьего века Сунь-цзы: ”В методах, которые употребляются при обычном счете, прежде всего [следует] познакомиться с разрядами: единицы вертикальны, десятки горизонтальны, сотни стоят, тысячи лежат, тысячи и десятки выглядят одинаково, десятки тысяч и сотни - тоже”. Сунь-цзы "Математический трактат”. Перевод Э.И.Березкиной. "Из истории физико-математических наук в станах Востока”, 1963, вып. 3, 23 . Слова Сунь-цзы о применении десятичной системы счисления в Китае напоминают мне один к одному о шумерской клинописи только для шестидесятеричной системы. Традиция использования счетных палочек в Китае воспрепятствовала проникновению в страну игр переноса, но может быть, благодаря этой традиции появилась "Книга перемен” и такие игры как домино и маджонг.
Компьютер и игры переноса.
В 1971 году в журнале "Наука и жизнь"№12 были опубликованы статьи "Игры и математика", "Машины играют в калах", в которых сотрудники Ленинградского Университета Андрей Аверьянович Аникеич, Гарольд Григорьевич Григорьев, спец. кор. Ю. Побожий рассказали об использовании древней игры для разработки компьютерных программ. Ученых привлекла в каллахе простота математической модели игры для целей програмирования. Игра в калах между машиной и человеком впервые показала,что компьютер может побеждать. В это время шахматные программы играли ещё слабо и не могли соревноваться с мастерами.
В настоящее время в интернете можно найти разные программы для игр переноса, если в поисковых системах ввести ключевые слова: "ВАРИ","МАНКАЛА","КАЛАХ".
Резюме:
Счётные доски с лунками, имевшие широкое распространение в древних цивилизациях, оставили после себя ряд игр на досках (с лунками, расположенными по тому же принципу, что и на счетных досках). Игры переноса являются ярким доказательством развития человеческой мысли более пяти тысяч лет назад, показывают развитие математики (разные системы счисления; математические действия, позиционные системы записи чисел) и применение систем измерения, привязанных к системе лунок счетных досок. Культура древних игр переноса переплелась с историей возникновения шахмат. Идея "дхармачакр” воплотилась и в игре переноса "рума” и в игре "чатуранга”. Надеюсь, что те читатели, которые интересуются в основном играми, теперь более ясно представляют, с чего началась история математики. По старинному изречению, как ребенок при рождении, так и начало математики — это чистая доска "tabula rasa”. Первым математиком был тот, кто первым положил на эту доску камушек "calculi”. Наши далекие предки несколько тысяч лет назад владели абстрактным мышлением и использовали его не только для выживания, но и для игры.